Activity 01
Summary
Make different geometric shapes (square, rectangle, triangle) from sheet of paper and explore the relations between them.
Warmup - 15 minutes
As this is the first class of the course, it would be nice to do some warm up and get the students excited.
Ask the students what origami they know and ask them to fold their favorite origami model.
The teacher can fold a grass hopper and a paper crane.
Activity - 1 hour
Make a square out of an A4 sheet and start exploration from the square.
Exploration 1 - Dividing square into two equal parts
Can you fold the square into two equal parts? How many different ways can you do it? What are the resulting shapes after folding?
Option 1: Rectangle Option 2: Right angled triangle
As you can see you are dividing the square into two halves. What property of the square is getting halved? Is it the length or perimeter or something else?
What is the perimeter of the rectangle and what is the perimeter of the triangle?
Can you make a square of half size from the given square?
Exploration 2 - The Classic Masu Box
TODO
Conversation in the Class
These are A4 sheets. Please take one each. Make that into two halves.
Take one of them and cut it as a square.
Dividing Square into two equal parts
All of you have a square sheet of paper with you. Can you fold that into two equal parts.
Oh, that is easy.
How many different ways can you do it?
Two ways. Horizontally/vertically and diagonally.
We can also fold it somewhere in the middle.
How many different ways can you do it?
Quite a lot.
And how do you decide where to fold?
I think any line going through the center of the square will work.
Wow, that is very interesting discovery. Can you try folding that and see if it actually works?
(Students fold the square, cut into two parts using an arbitrary line going through the center).
It seems to be working.
Alright. What were the possible resulting shapes when you fold a square into two equal parts?
A rectangle, a triangle and some odd shape.
Lets look at the rectangle. If the square had a side length of 2 units, what would be the dimensions of the rectangle?
2x1
Lets look at the triangle. What kind of triangle is it?
Right angled.
And?
Equilateral.
No, right angled triangle can not be equilateral.
It also and isosceles triangle.
Yes, this is right-angled and isosceles triangle. Do you know anything about the lengths of sides?
The two short sides are 2 and 2, same as in the square.
What about the longest side?
I think it will be one and half times the short one.
Are you sure?
No, I think it will be about 1.4.
No... that is too much math!
Ok. We don't yet know what is the longest side. We'll come back to it.
Can you fold the square into two equal parts such that the resulting shape is also a square?
That is not possible...
What if we fold the corners... I got it!
Are you sure it is half of the original square?
Yes, of course.
So, what property of square are we dividing into half? Is it the side, the perimeter or something else?
The perimeter (very confidently).
Let's find out. If the side of the original square is 2 units, what is perimeter of the square?
8
Let's consider the first way where you folded the square into two rectangles. What is the perimeter of the rectangle?
1, 2, 1, 2. That is 6.
Was it half?
No.
Let's look at the triangle. What is the perimeter?
The short sides are 2 each.
And the longest side?
May be 1.5. I mean 1.5 times 2.
Ok. We don't that exactly, but that is surely more than 2. So the perimeter of the triangle is actually more that of the rectangle. Do you agree?
Yes.
You can see that we are halving the perimeter. What is the property that we are making into two halves?
It is area.
What is the area of the original square?
It is 2x2 that is 4.
What is the area of the rectangle that you got after folding?
That is 2 x 1, which is 2.
Alright! Let's fold something more interesting now.
The Classic Masu Box
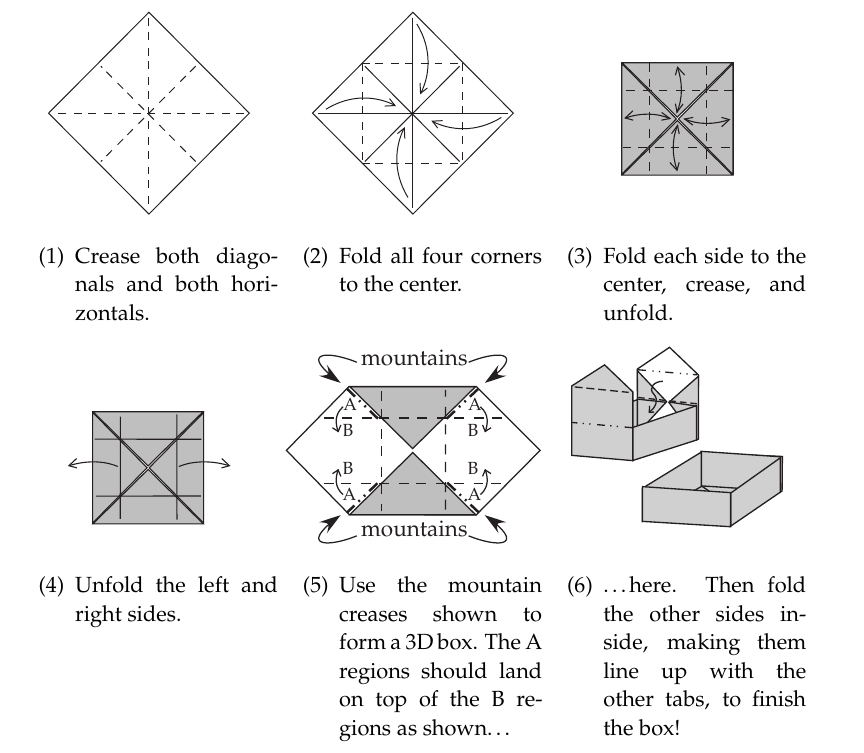
(showed how to make this box and asked everyone to make it)
If we have to make a box of size 10cm x 10 cm, what should be the size of the original square paper? Isn't that an interesting to know how to solve it?
Lets open the box and see. (see the top right diagram in the picture above). The center is the base of the box. What portion it is in the whole?
There are 4 small cells in the base and there are 16 of them in total. That makes the bigger square times the base of the box.
Now let's look at the sides. The side of the bigger square is twice as big as the base of the box.
So, if we increase the side by 2, the area grows by a factor of 4!
What happens to the area if we increase the side by 3 times?
It will be 6 times?
Are you sure? Let's find it out by folding a paper.
Do you see?
It is 9 times, not 6 times.
Yes, it increases 3 times both horizontally and vertically. So the area grows by a factor of .
What happens to the area if we increase the side by 4 times?
It grows by 16 times!
Wonderful!
Now tell me this. What happens to the side if I increase the area by 4 times?
It will increase by two times.
What will happen to the side if I increase the area by 9 times?
It will increase by three times.
Awesome! How are you getting that?
Oh, we are taking the square root.
Interesting! What happens to the side if I increase the area by 2?
It will be... it will be... square root of two!
What is that value? What is square root of two.
We don't have to know what it is. Let's call it square-root-of-two.
...
(we opened the box and understood that the area of the starting square of paper is 8 times the base of the box. So the side of the starting square is times the side of the box base.)