Math Activity

This book is the notes from the Math Activity course taught by Anand Chitipothu at Center for Learning during Jan-Mar 2025.

The goal of the course is to explore mathematics through Origami.

During the course, we would like to do the following:

• Explore math through origami
• Ask interesting math questions using paper folding
• Fold something interesting every day
• Make something grand together by the end of the course

Activity 01

Summary

Make different geometric shapes (square, rectangle, triangle) from sheet of paper and explore the relations between them.

Warmup - 15 minutes

As this is the first class of the course, it would be nice to do some warm up and get the students excited.

Ask the students what origami they know and ask them to fold their favorite origami model.

The teacher can fold a grass hopper and a paper crane.

Activity - 1 hour

Make a square out of an A4 sheet and start exploration from the square.

Exploration 1 - Dividing square into two equal parts

Can you fold the square into two equal parts? How many different ways can you do it? What are the resulting shapes after folding?

Option 1: Rectangle Option 2: Right angled triangle

As you can see you are dividing the square into two halves. What property of the square is getting halved? Is it the length or perimeter or something else?

What is the perimeter of the rectangle and what is the perimeter of the triangle?

Can you make a square of half size from the given square?

Exploration 2 - The Classic Masu Box

TODO

Conversation in the Class

These are A4 sheets. Please take one each. Make that into two halves.

Take one of them and cut it as a square.

Dividing Square into two equal parts

All of you have a square sheet of paper with you. Can you fold that into two equal parts.

Oh, that is easy.

How many different ways can you do it?

Two ways. Horizontally/vertically and diagonally.

We can also fold it somewhere in the middle.

How many different ways can you do it?

Quite a lot.

And how do you decide where to fold?

I think any line going through the center of the square will work.

Wow, that is very interesting discovery. Can you try folding that and see if it actually works?

(Students fold the square, cut into two parts using an arbitrary line going through the center).

It seems to be working.

Alright. What were the possible resulting shapes when you fold a square into two equal parts?

A rectangle, a triangle and some odd shape.

Lets look at the rectangle. If the square had a side length of 2 units, what would be the dimensions of the rectangle?

2x1

Lets look at the triangle. What kind of triangle is it?

Right angled.

And?

Equilateral.

No, right angled triangle can not be equilateral.

It also and isosceles triangle.

Yes, this is right-angled and isosceles triangle. Do you know anything about the lengths of sides?

The two short sides are 2 and 2, same as in the square.

What about the longest side?

I think it will be one and half times the short one.

Are you sure?

No, I think it will be about 1.4.

No... that is too much math!

Ok. We don't yet know what is the longest side. We'll come back to it.

Can you fold the square into two equal parts such that the resulting shape is also a square?

That is not possible...

What if we fold the corners... I got it!

Are you sure it is half of the original square?

Yes, of course.

So, what property of square are we dividing into half? Is it the side, the perimeter or something else?

The perimeter (very confidently).

Let's find out. If the side of the original square is 2 units, what is perimeter of the square?

8

Let's consider the first way where you folded the square into two rectangles. What is the perimeter of the rectangle?

1, 2, 1, 2. That is 6.

Was it half?

No.

Let's look at the triangle. What is the perimeter?

The short sides are 2 each.

And the longest side?

May be 1.5. I mean 1.5 times 2.

Ok. We don't that exactly, but that is surely more than 2. So the perimeter of the triangle is actually more that of the rectangle. Do you agree?

Yes.

You can see that we are halving the perimeter. What is the property that we are making into two halves?

It is area.

What is the area of the original square?

It is 2x2 that is 4.

What is the area of the rectangle that you got after folding?

That is 2 x 1, which is 2.

Alright! Let's fold something more interesting now.

The Classic Masu Box

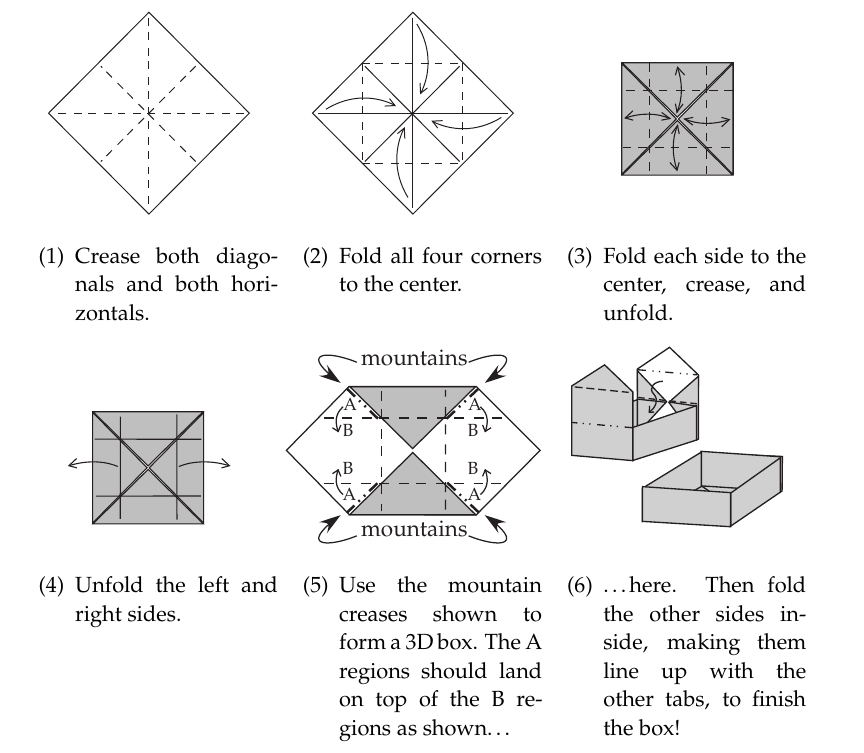
(showed how to make this box and asked everyone to make it)

If we have to make a box of size 10cm x 10 cm, what should be the size of the original square paper? Isn't that an interesting to know how to solve it?

Lets open the box and see. (see the top right diagram in the picture above). The center is the base of the box. What portion it is in the whole?

There are 4 small cells in the base and there are 16 of them in total. That makes the bigger square $4$ times the base of the box.

Now let's look at the sides. The side of the bigger square is twice as big as the base of the box.

So, if we increase the side by 2, the area grows by a factor of 4!

What happens to the area if we increase the side by 3 times?

It will be 6 times?

Are you sure? Let's find it out by folding a paper.

Do you see?

It is 9 times, not 6 times.

Yes, it increases 3 times both horizontally and vertically. So the area grows by a factor of $3x3$.

What happens to the area if we increase the side by 4 times?

It grows by 16 times!

Wonderful!

Now tell me this. What happens to the side if I increase the area by 4 times?

It will increase by two times.

What will happen to the side if I increase the area by 9 times?

It will increase by three times.

Awesome! How are you getting that?

Oh, we are taking the square root.

Interesting! What happens to the side if I increase the area by 2?

It will be... it will be... square root of two!

What is that value? What is square root of two.

We don't have to know what it is. Let's call it square-root-of-two.

...

(we opened the box and understood that the area of the starting square of paper is 8 times the base of the box. So the side of the starting square is $2\sqrt{2}$ times the side of the box base.)

Activity 02

Summary

• Continuing exploring the concept of $\sqrt{2}$ using proportions of an A4 sheet.
• understand mountan folds and valley folds
• make a model of octahedron skeleton and introduce the concepts of regular polyhedron and volume
• thread the octahedron model and hang it

Materials Required

• A4 sheets (about 3 sheets per student)
• 3"x3" squares of color origami paper. Each student needs 2 of each of 3 colors

Warmup - 10 mins

Review the masu box made during the [[activity-01]] and recap the relation between the side of the box to the area of the original square.

Activity - 60 mins

Exploration 1: Similarity of rectangles

How do you tell if two rectangles (this could be just a paper, or a book, or a phone) are similar?

• Case 1: A square and a rectangle with a long edge
• Case 2: A4 and A5 sheets

How do you define similarity?

Can you figure out how to tell if two rectangles are similar?

Have you noticed if we divide and A4 sheet into two equal parts along the long edge, we get a similar shape. Is that true for any size of paper? What is the magic portion of the A4 sheet that makes this possible?

Exploration 2: Mountain and valley folds

Make a waterbomb base. Mark the mountain and valley folds.

TODO

Exploration 3: Octahedron Skeleton

TODO

Activity 03

Similar triangles and dividing a paper into one third.

Origami Model

Modular Cube

Activity 04 - Irrational Excursions

Overview

Explore folding irrational numbers on paper.

Used a worksheet to explore $\sqrt{3}$ and $\sqrt{5}$ in triangles.

Origami model

Modular Origami ring.

Activity 12 from Project Origami.

Notes

Below are some origami instructions. Take a square and make a crease folding it in half vertically. Make a crease that connects the mid point of the top edge and the bottom right corner.

Assuming the side of square is 2 units, find the length of the line AC.

Activity 05

Overview

Explore 90-60-30 triangle and used that to fold an equilateral triangle.

Establish that 90-60-30 triangle always has a ratio of $\frac{1}{2}$ and 90-45-45 triangle always has ratio of $\frac{1}{\sqrt{2}}$. Use that to briefly introduce sine and cosine.

Use the established fact that a 90-60-30 triangle has a ratio of $\frac{1}{2}$, to fold an equilateral triangle on a square sheet of paper.

Origami Model

Hexaflexagon

Notes

There were three parts in this activity.

1. Solving the worksheet to establish the properties of 90-60-30 triangles
2. Folding an equilateral triangle on a square sheet of paper
3. Hexaflexagons

Last line!

Activity 06

Overview

Explore the ratios of sides of right angled triangles and establish the sin and cos notation.

Learn how to fold a rectangle with proportions $1:\sqrt{3}$.

Origami Model

A Star in All of Us Designed by Mukul Achawal Diagrammed by Sara Adams

https://www.happyfolding.com/files/achawal-a_star_in_all_of_us.pdf

Overview

Explore the angles of a regular pentagon and learn how to cut a regular pentagon from a square sheet of paper.

Origami Model

Folded phizz units and make a 30-unit bucky ball

Didn't do this one.

Sakura Star, designed Ali Bahmani, and folded by Sara Adams https://www.happyfolding.com/instructions-bahmani-sakura_star

Activity 08

Notes

Notes about interesting resources, thoughts and ideas about math-activity.

Mon Feb 24, 2025

Make a hyperbolic football

Planning to explore platonic solids in the next class.

Sun Feb 09, 2025

Origami Pythagorean spiral https://www.happyfolding.com/gallery-pythagorean_spiral

Wed Feb 05, 2025

Today's class went well.

D & E are having trouble focusing on the class and paying attention to folding paper. Everyone else seems to be doing well.

None of them have the first worksheet with them. This time, I kept the solved worksheets with me.

They have figured out that the triangle is a 90-60-30 triangle, but they weren't able to prove it. I told them that we'll get back to it later. I need to take it up in the next class.

Tue Jan 28, 2025

Proving Pythagoras theorem using Origami.

Origami Proof of Pythagoras theorem by Vi Hart (YouTube)

Origami Instructions to use origami to prove the Pythagorean Theorem (PDF).

We could use this to prove $(a+b{)}^2=a^2+b^2+2ab$ and Pythagoras theorem $a^2+b^2=c^2$.

It would be interesting to challenge them to fold $\sqrt{3}$, $\sqrt{5}$ etc.

Sun Jan 26, 2025

Came across a paper discussing about impact of origami instruction on spacial visualization skills of students.

Origami Instruction in the Middle School Mathematics Classroom: Its Impact on Spatial Visualization and Geometry Knowledge of Students, RMLE Online, Vol. 32, No. 7

I learnt about the topic of Spacial Visualization Skills and measuring them. Looks like there is a quite a bit of research on this topic in connection with learning math. Something to worth exploring.

Also found a doctoral thesis of Norma. J. Boakes on the topic

Other resources:

• Spacial Reasoning Instrument - a questionnaire to survey spatial reasoning ability (PDF)

Sat Jan 25, 2025

Had a call with Zeus.

I have told about my concern that the students are not making any notes. He suggested that giving worksheets with questions to answer may be a good way to address that.